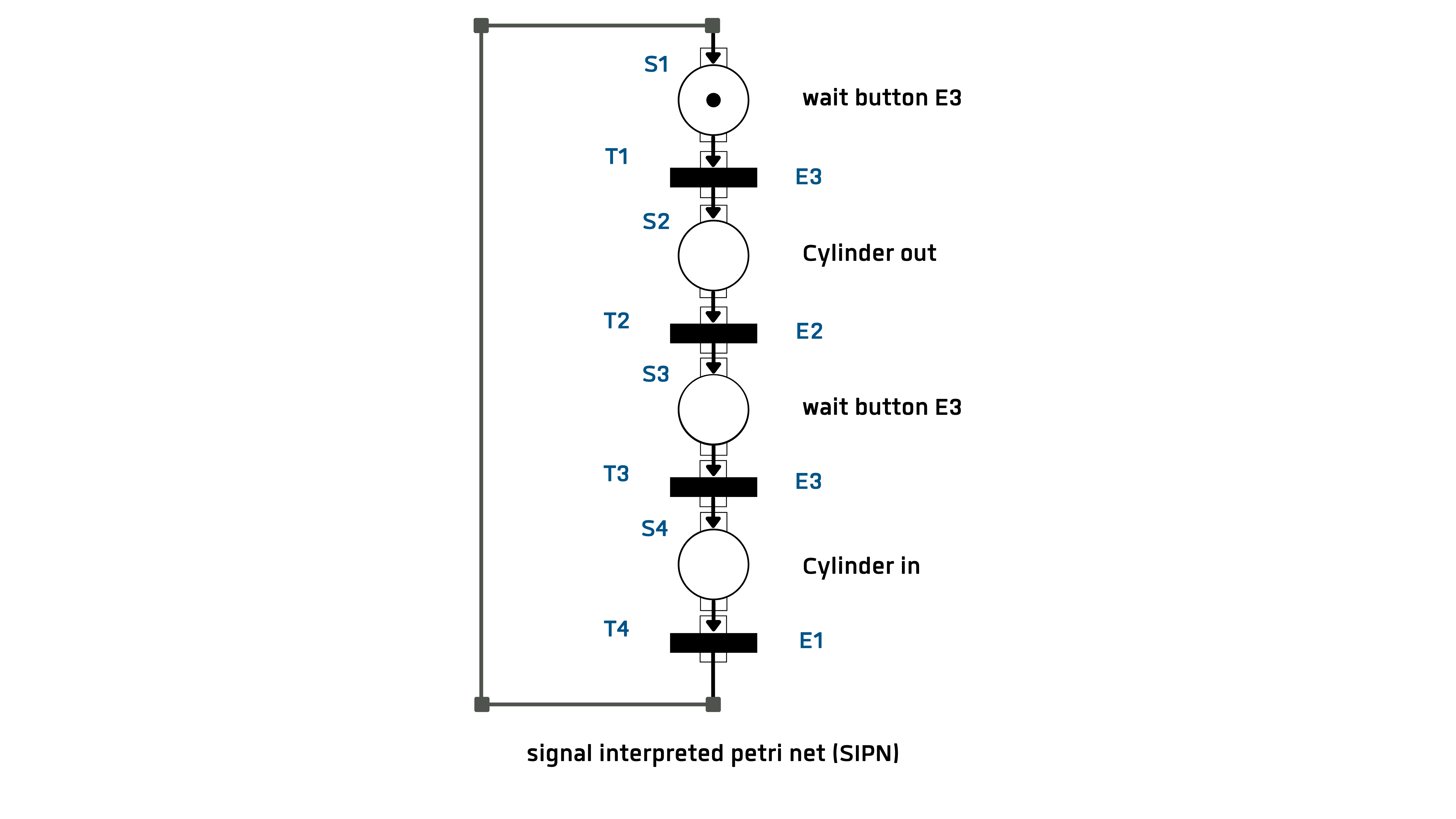
The Petri net is a bipartite digraph with places and transitions as nodes. Bipartite refers to the property of the net of having two disjoint subsets of nodes, namely the
places or locations (represented by the circles) and
transitions (represented by dashes or rectangles).
Digraph means directed graph, which always connects nodes of different types. You may connect any number of nodes of one kind with any number of nodes of the other kind.
Places and transitions are numbered or labelled with a text. A transition cannot accommodate a marker. In Figure 7-4, place S1 is given the initial mark. This mark jumps to the next place when the transition condition is fulfilled. Each transition receives a switching condition, which can be a Boolean function of all input signals. When a marker has reached a position, the defined outputs are activated. A detailed description of the SIPN is not given here, but reference is made to the following literature. (Litz L. , 2005); (Lunze, 2003).
The input vector for the control example is:
eT = [E1 E2 E3] = [ eT = [E1 E2 E3] = [ rear cylinder front cylinder key];
The output vector for the control example is:
aT = [A1 A2] = [Valve cyl._before Valve cyl_back]
The switching conditions of the transitions are:
SB(T1) = E3
SB(T2) = E2
SB(T3) = E3
SB(T4) = E1
The output variables at the points are:
aTS1 = {0 0}; aTS2 = {1 0}; aTS3 = {0 0}; aTS4 = {0 1};
